Muoto, jonka evoluutio löysi ja hylkäsi
Teksti: Heikki Simola ja Rasmus Ojala
Kuvat: Tomi Setälä
Monet elämänmuodot ovat kauniita. Erityinen kauneuden luokka on matemaattisten muotojen kauneus. Logaritminen spiraali kuuluu kiistatta kauniiden matemaattisten muotojen joukkoon. Puhtaana muotona se on elävässä luonnossa harvinainen. Nykyään elävistä lajeista vain muutamien nilviäisten, ja nimenomaan pääjalkaisten eli mustekalojen luokkaan kuuluvien lajien kuoret kasvavat puhtaan logaritmispiraalin mukaisesti.
Tosielämän Nautilus
Tunnetuin logaritmisen spiraalin muotoinen kuori lienee Nautilus-helmiveneellä. Nautilus-lajit ovat trooppisten merien eläjiä, jotka viihtyvät tyypillisesti 200–500 metrin syvyydessä. Ne ovat rakenteeltaan melko alkukantaisia muihin nykyisiin mustekalojen ryhmän lajeihin verrattuna. Niillä on tarttuma- ja liikuntaeliminä kymmeniä yksinkertaisia ja lyhyehköjä lonkeroita, joiden keskellä on nokkamainen suu. Todennäköisesti tämäntapainen ruumiinrakenne on ollut myös ammoin sukupuuttoon kuolleilla ammoniiteilla, joita eleli maapallon merissä devonikaudelta aina liitukaudelle asti. Nautilus-helmiveneet edustavat ammoniiteille rinnakkaista kehityshistoriallista linjaa, ja ovat pääjalkaisten luokassa sukua lähinnä oikosarvisille. Nautilidae-heimo tunnetaan fossiileina triaskauden lopulta, eli runsaan 200 miljoonan vuoden takaa.

Nautilus-helmiveneen kuori kiertyy logaritmisesti keskipisteensä ympäri.
Toisenlainen puhdas logaritminen spiraali muodostuu Argonauta-paperiveneiden ohueeseen kalkkikuoreen. Argonauta-lajit kuuluvat kahdeksanlonkeroisiin mustekaloihin ja elävät lämpimien merien pintakerroksissa, siis planktisesti, toisin kuin useimmat mustekalat, jotka elävät pohjan läheisyydessä. Suurin laji, Argonauta argo, voi kasvattaa jopa yli 20 senttimetrin läpimittaisia ’paperiveneitä’, joita onnekas etsijä saattaa löytää lämpimien merien rannoille ajautuneena.
Ainoastaan naarasyksilöille kehittyvä hento kuori kasvaa kahden erikoistuneen lonkeron erittämänä ikään kuin ulkopuolisena rakenteena. Kasvutapa on siis erilainen kuin muilla kuorellisilla nilviäisillä, joilla kuoren reuna kasvaa eläimen vartalon tai sitä ympäröivän vaipan pinnasta, ja eläin elää pysyvästi kuorensa sisällä. Argonauta-naaras pysyttelee kuorensa suojassa, mutta pystyy myös halutessaan pujottautumaan siitä ulos. Kuori toimii suojana naaraan hautomille munille ja kehittyville poikasille. Kuoren sisällä on yleensä ilmakupla, jonka avulla eläin pystyy säätelemään keijumistaan sopivalle syvyydelle.
Syvän meren arvoitus

Eräillä kotiloilla on kuoressaan erillinen luukku, operculum, jonka kotilo voi vetää kiinni kuin oven vetäytyessään kuoreensa. Operculum kasvaa samaa tahtia kuin kuori, ja sen kierteinen kasvu näkyy logaritmisen spiraalin muotoisena saumana luukun pinnassa.
Vielä kolmaskin logaritminen spiraali löytyy pääjalkaisten ryhmästä: niin ikään trooppisten merien planktoniin kuuluva Spirula spirula. Tämä arvoituksellinen laji – lahkonsa ainoa – on suuren Carl von Linnén nimeämä, vaikka tuohon aikaan ei vielä tiedetty, minkälainen otus näitä rannoilta löytyviä hentoja kuoria kasvattaa. Kyseessä on pieni mustekala, joka elää jopa satojen metrien syvyydessä. Kierteinen kuori on sisäinen tukiranka ja toimii myös kelluntaelimenä.
Spirula-ranka kasvaa avoimena kierteenä, eli kierteet eivät kosketa toisiaan. Väliseinineen ja niitä lävistävine huokosineen se muistuttaa rakenteeltaan Nautilus-kuoria, samoin fossiilisten ammoniittien ja oikosarvisten rakennetta. Spirula-kuori kuitenkin kiertyy toiseen suuntaan: kierre aukeaa alaspäin, kun ammoniittien ja Nautilus-lajien kierre avautuu alhaalta ylöspäin.
Tässä kuvatut kuoret ovat yhdessä tasossa kiertyviä spiraaleja. Logaritmisena spiraalina kasvavia kuoria on myös muilla nilviäisillä, mutta niissä muotoon vaikuttaa lisäksi kiraliteetti eli kätisyys, toisin sanoen kuori kiertyy kartiomaisesti, ruuvikierteen tapaan vasemmalle tai oikealle. Se ei siis kierrä keskipisteensä vaan pituusakselinsa ympäri. Tällaisia ovat useimmat kotiloiden kuoret.
Spiraalin haasteet
On kiinnostava pohtia, miksi nimenomaan perusmuotoinen tasospiraali on suorastaan äärimmäisen harvinainen nykyään elävien eläinten rakenteena. Selitys lienee siinä, että sinänsä kaunis kasvutapa on myös ehdottoman kaavamainen ja pakottaa yksilön tasaisesti kiihtyvään kasvuun. Spiraalikierteen logaritminen kasvu merkitsee ruumiinkoossa kuutiollista lisäystä.
Tällainen kasvukäyrä on ongelmallinen, koska mikä tahansa evoluution synnyttämä toiminnallisen anatomian kokonaisuus on yleensä optimaalinen vain tietyissä kokorajoissa. Logaritmisessa kasvumallissa optimaalinen koko ohitetaan nopeasti, minkä jälkeen yksilön käy yhä vaikeammaksi hankkia riittävästi ravintoa kiihtyvän kasvunsa ylläpitoon. Seurauksena on nääntyminen nälkään.
Kotiloiden parempaa menestystä selittänee se, että kartiomainen kasvutapa lieventää logaritmisen kasvun ongelmaa. Kotilon kuorelle riittää avautuminen paljon pienemmässä kulmassa kuin tyypilliselle ammoniitin tasokierteelle, jolloin kuoren muoto säilyy suppeana ja eläin on toiminnallisesti suotuisassa koossa suhteellisesti suuremman osan elämästään. Monilla kotiloilla kasvu myös hidastuu, kun tietty koko on saavutettu. Puhtaassa logaritmisessa kasvussa mitään tällaista säätelyä ei ilmene.
Ammoniittien kukoistuskausi voidaan nähdä kauniina jaksona elämän kehityksen historiaa: kalkkikuoren spiraalimainen kasvutapa uutena innovaationa johti ammoniittien kukoistukseen lähes 200 miljoonaksi vuodeksi. Aikaa myöten evoluutio tuotti uusia parempia malleja, ja logaritmispiraalit syrjäytyivät lähes täydellisesti. Kauniiden fossiilien ohella voimme kuitenkin iloita siitä, että sentään muutama puhtaan logaritmispiraalin kantaja on edelleen jäljellä planeettamme ihmeellisten elämänmuotojen joukossa.
Seuraavalla videolla pääset tutustumaan logaritmisen spiraalin muotoiseen Nautilus-helmiveneeseen.
Kultainen spiraali – erikoistapaus
Argonauta argo: Tomi Setälä, spiraali: Wikimedia Commons
Logaritminen spiraali on päättymätön, tietyn pisteen ympäri kiertyvä viiva, jonka avautumiskulma on vakio. Toisin sanoen spiraalin tangentti eli sivuaja on joka kohdassa samassa kulmassa keskipisteestä piirrettyyn säteeseen nähden. Logaritmisen spiraalin yhtälö voidaan niin kutsutussa napakoordinaatistossa esittää muodossa r = ecϑ
jossa r on etäisyys keskipisteestä eli säde, e on luonnollisen logaritmijärjestelmän kantaluku, ϑ (theta) on kiertokulma ja c on avautumiskulman määrittävä vakio.
Logaritminen spiraali kasvaa ulospäin yhä laajenevina kehinä äärettömiin, mutta käyrä on päättymätön myös sisäänpäin kiertyessään. Keskipistettään eli origoa matemaattinen kuvaaja ei koskaan saavuta (vaikka piirroskuvassa viivan paksuus tuleekin vastaan ja viiva näyttää päättyvän pisteeseen).
Nimitystä kultainen spiraali voidaan käyttää logaritmisesta spiraalista, jonka mittasuhteista löytyy jatkuva suhde eli niin kutsuttu kultainen leikkaus. Kultaista leikkausta kuvataan yhtälöllä a:b = b:(a+b); sen likiarvo on 1,618, ja sitä merkitään usein symbolilla φ (fii). Yhtälö siis toteutuu, kun a = 0,618, b = 1 ja (a+b) on 1,618. Tekijän c arvolla 0,0053468 spiraaliyhtälö toteutuu siten, että jokaisella neljänneskierroksella (90 astetta) säde kasvaa kultaisen suhteen φ verran.
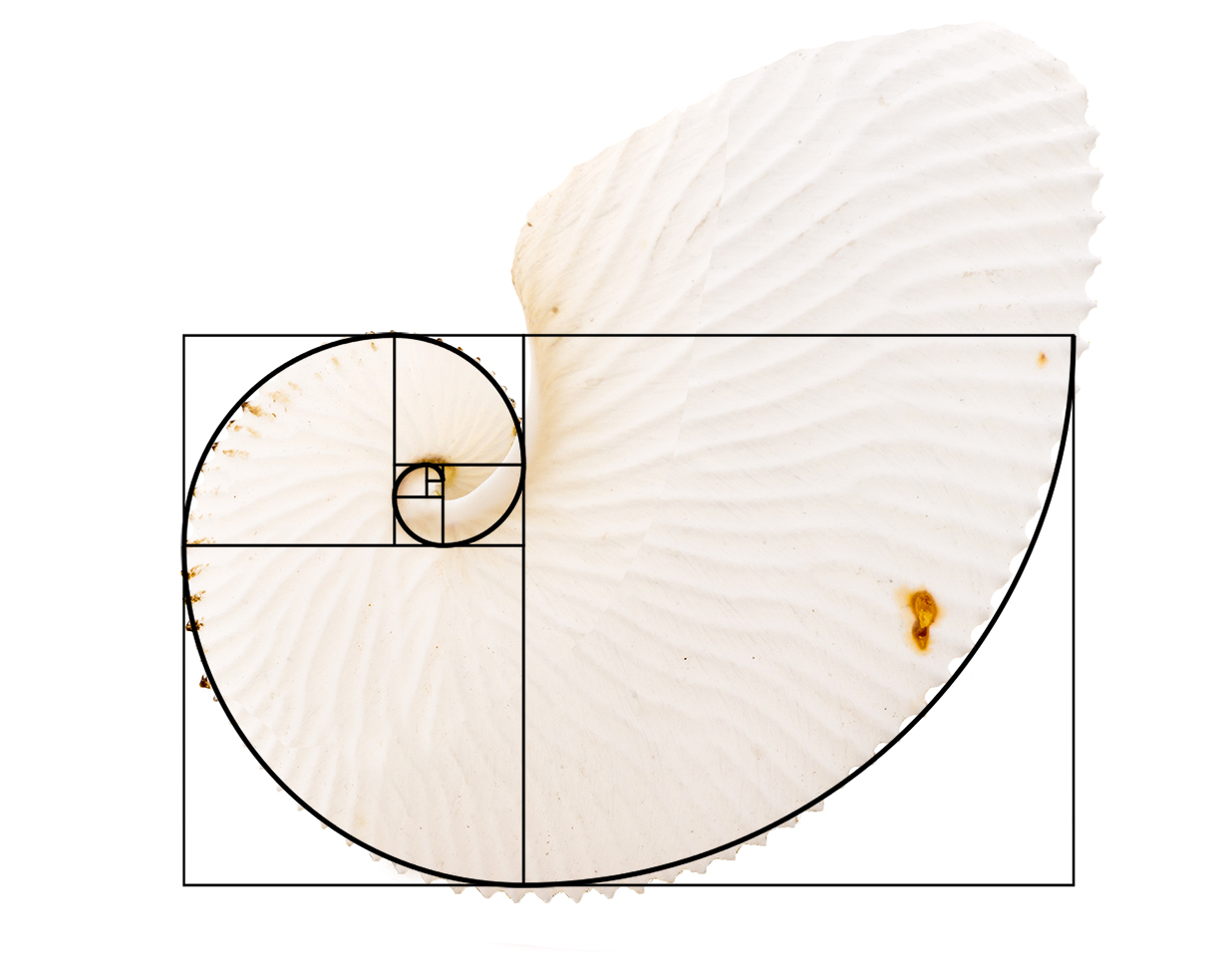
Varsin tyydyttävä kultaisen spiraalin muotoa lähenevä käyrä voidaan piirtää tavalliselle ruutupaperille Fibonaccin lukusarjaa käyttäen. Tätä havainnollistaa oheinen kuva. Fibonacci-sarjassa, 1, 1, 2, 3, 5, 8, 13 ja niin edelleen, seuraava luku on aina kahden edellisen summa, joten peräkkäisten lukujen suhde lähenee kultaista suhdetta. Kun piirretään neliöitä sarjaksi, jossa sivun pituus kasvaa Fibonacci-lukujen mukaan, ja harpilla piirretään kunkin uuden neliön sisään sen sivun säteinen ympyränkaaren neljännes, saadaan kultaista spiraalia lähenevä käyrä. Argonauta argo -paperiveneen kuoren muoto noudattaa lähes täydellisesti tätä spiraalia.
Kirjoittajista Heikki Simola on biologi, joka keräilee fossiileja. Rasmus Ojala on matematiikasta ja fysiikasta kiinnostunut opiskelija.



